Wang Tiles

Tiles

We can generate a simply by generating four random numbers - one for each tile edge - in the range 0 to colors with colors being the number of possible colors we want to allow. We can then map those random numbers to acutal colors and plot the tile for however many tiles we want.

from random import choice, seed, shuffle
import matplotlib.pyplot as plt
from itertools import product
import numpy as np

def generate_random_tile_set(tiles, colors, state=None):
    np.random.seed(state)
    return np.random.randint(0, colors, size=(tiles, 4))

def plot_tile_set(tiles, palette='viridis'):
    num_tiles, num_colors = tiles.shape[0], tiles.max() + 1
    fig, axs = plt.subplots(1, num_tiles)
    cmap = plt.cm.get_cmap(palette, num_colors)

    for tile, ax in zip(tiles, axs):
        edges = [
            plt.Polygon([[1, 1], [0, 1], [0.5, 0.5]], fc=cmap(tile[0])),
            plt.Polygon([[1, 0], [1, 1], [0.5, 0.5]], fc=cmap(tile[1])),
            plt.Polygon([[0, 0], [1, 0], [0.5, 0.5]], fc=cmap(tile[2])),
            plt.Polygon([[0, 1], [0, 0], [0.5, 0.5]], fc=cmap(tile[3]))
        ]

        for edge in edges:
            ax.add_patch(edge)

        ax.set_aspect('equal')
        ax.axis('off')
    
    return fig

plt.show(plot_tile_set(generate_random_tile_set(6, 3, state=69)))

Placement

We tile from top left to bottom right, so when we place a tile, we need to make sure that the color on the bottom edge of the tile above and the right edge of the tile to the left will match with the tile we want to place. tile_candidates will give us all the tiles that adhere to the rules for a specific position in the grid using the checks described.

def tile_candidates(tiles, grid, i, j, unordered=False):
    above = grid[i - 1, j, 2] if i > 0 else -1
    left = grid[i, j - 1, 1] if j > 0 else -1
    if above >= 0 and left >= 0:
        candidates = [tile for tile in tiles if tile[0] == above and tile[3] == left]
    elif above >= 0:
        candidates = [tile for tile in tiles if tile[0] == above]
    elif left >= 0:
        candidates = [tile for tile in tiles if tile[3] == left]
    else:
        candidates = [tile for tile in tiles]
    if unordered:
        shuffle(candidates)
    return candidates
    
def tile_grid(tiles, width, height, state=None):
    if state: seed(state)
    grid = np.empty((height, width, 4), dtype=int)
    for i in range(height):
        for j in range(width):
            grid[i, j] = choice(tile_candidates(tiles, grid, i, j))      
    return grid

def plot_tile_grid(grid, palette='viridis'):
    num_colors = grid.max() + 1
    cmap = plt.cm.get_cmap(palette, num_colors)
    fig, axs = plt.subplots(grid.shape[0], grid.shape[1], figsize=(grid.shape[1], grid.shape[0]))

    for ax, (i, j) in zip(axs.flat, np.ndindex(grid.shape[:2])):
        edges = [
            plt.Polygon([[1, 1], [0, 1], [0.5, 0.5]], fc=cmap(grid[i, j, 0])),
            plt.Polygon([[1, 0], [1, 1], [0.5, 0.5]], fc=cmap(grid[i, j, 1])),
            plt.Polygon([[0, 0], [1, 0], [0.5, 0.5]], fc=cmap(grid[i, j, 2])),
            plt.Polygon([[0, 1], [0, 0], [0.5, 0.5]], fc=cmap(grid[i, j, 3]))
        ]

        for edge in edges:
            ax.add_patch(edge)

        ax.set_aspect('equal')
        ax.axis('off')
        
    plt.subplots_adjust(wspace=0.03, hspace=0.03)
    
    return fig

tiles = np.array([[0, 0, 1, 1],[1, 1, 0, 0]])
plt.show(plot_tile_grid(tile_grid(tiles, 32, 8)))

def generate_complete_tile_set(colors):
    return np.array(list(product(range(colors), repeat=4)))

tiles = generate_complete_tile_set(2)
plt.show(plot_tile_set(tiles))
plt.show(plot_tile_grid(tile_grid(tiles, 64, 32, state=42)))

plt.show(plot_tile_grid(tile_grid(generate_complete_tile_set(4), 128, 32, state=42)))

Backtracking

The previous tile placement algorithm can fail even if a solution exists given an incomplete tile set because it can effectively ‘paint itself into a corner’. The following algorithms avoids this using a backtracking strategy to ensure a correct tile placement is generated if possible for a given tileset. If we find that we have placed a series of tiles such that no tiles from the set can be placed subsequently, we undo the previous tile and try again.

def backtracking(tiles, grid, y=0, x=0, offset=0, unordered=False):
    if y == grid.shape[0]:
        return grid
    
    if x == grid.shape[1]:
        return backtracking(tiles, grid, y+1, offset, offset, unordered)
    
    candidates = tile_candidates(tiles, grid, y, x, unordered)

    for tile in candidates:
        grid[y, x] = tile
        result = backtracking(tiles, grid, y, x+1, offset, unordered)
        if result is not None:
            return result
        grid[y, x] = np.ones(4, dtype=int)
        
    return None

def tile_grid_exhaustive(tiles, width, height, state=None):
    grid = np.empty((height, width, 4), dtype=int)
    
    if state:
        seed(state)
        
    return backtracking(tiles, grid, unordered=state is not None)

tiles = generate_random_tile_set(6, 2, state=7983)
plt.show(plot_tile_set(tiles))
plt.show(plot_tile_grid(tile_grid_exhaustive(tiles, 16, 8, state=9178)))

tiles = generate_random_tile_set(8, 3, state=9781)
plt.show(plot_tile_set(tiles))
plt.show(plot_tile_grid(tile_grid_exhaustive(tiles, 16, 8, state=42)))

tiles = generate_random_tile_set(8, 4, state=9413)
plt.show(plot_tile_set(tiles))
plt.show(plot_tile_grid(tile_grid_exhaustive(tiles, 16, 8, state=6769)))

tiles = generate_random_tile_set(8, 5, state=34405)
plt.show(plot_tile_set(tiles))
plt.show(plot_tile_grid(tile_grid_exhaustive(tiles, 16, 8, state=69)))

Computation

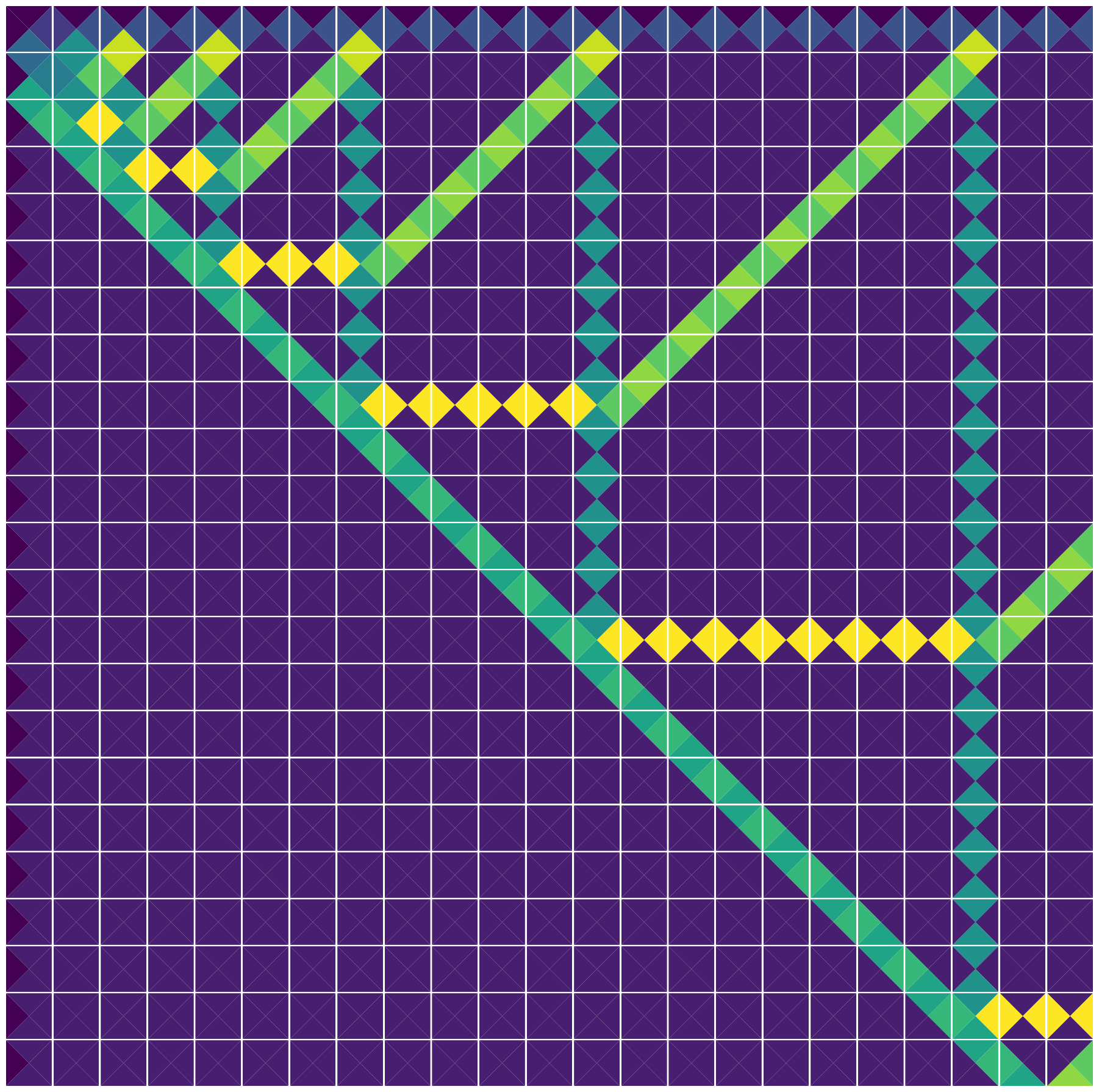
The following tile set can be arranged such that the computation of the Fibonacci sequence is encoded in the grid. The column indices (1-indexed) correspond to the elements of the sequence starting from 1. The grid shows 1, 2, 3, 5, 8, 13, 21…

B. Grünbaum and G. C. Shepard, “Tilings and Patterns,” W. H. Freeman and Company, New York, 1986.

tiles = np.array([
    [0, 2, 4, 0],
    [0, 3, 6, 2],
    [0, 3, 11, 3],
    [0, 3, 1, 3],
    [1, 1, 1, 0],
    [4, 5, 7, 0],
    [6, 9, 6, 12],
    [11, 1, 6, 9],
    [10, 1, 1, 9], 
    [1, 9, 10, 1],
    [6, 1, 6, 1],
    [7, 8, 1, 0],
    [7, 8, 1, 1],
    [1, 1, 7, 8],
    [6, 12, 7, 8],
    [1, 12, 1, 12],
    [6, 9, 6, 5],
    [1, 1, 1, 1]
])

grid = np.ones((24, 24, 4), dtype=int)
grid[0, :] = np.array([0, 0, 0, 0])
grid[:, 0] = np.array([0, 0, 0, 0])

grid = backtracking(tiles, grid, 1, 1, 1)

plt.show(plot_tile_grid(grid[1:, 1:]))